前言:
早几年前写博客的时候,编辑公式都是在线网站编辑的,有时候这个网站不稳定,贴的公式看不到。如果有需要,pdf版下载地址点击打开链接,给您阅读带来的不便表示抱歉,祝大家好运。
博主在自主学习粒子滤波的过程中,看了很多文献或博客,不知道是看文献时粗心大意还是悟性太低,看着那么多公式,总是无法把握住粒子滤波的思路,也无法将理论和实践对应起来。比如:理论推导过程中那么多概率公式,概率怎么和系统的状态变量对应上了?状态粒子是怎么一步步采样出来的,为什么程序里面都是直接用状态方程来计算?粒子的权重是怎么来的?经过一段时间的理解,总算理清了它的脉络。同时也觉得,只有对理论的推导心中有数了,才能知道什么样的地方可以用这个算法,以及这个算法有什么不足。因此,本文将结合实际程序给出粒子滤波的详细推导,在推导过程中加入博主自己的理解,如有不妥,请指出,谢谢。
文章架构:
由最基础的贝叶斯估计开始介绍,再引出蒙特卡罗采样,重要性采样,SIS粒子滤波,重采样,基本粒子滤波Generic Particle Filter,SIR粒子滤波,这些概念的引进,都是为了解决上一个概念中出现的问题而环环相扣的。最后给出几个在matlab和python中的应用,例程包括图像跟踪,滤波,机器人定位。
再往下看之前,也可以看看《卡尔曼滤波:从推导到应用》,好对这种通过状态方程来滤波的思路有所了解。
一、贝叶斯滤波
假设有一个系统,我们知道它的状态方程,和测量方程如下:
如:
(1)
如:
(2)
其中x为系统状态,y为测量到的数据,f,h是状态转移函数和测量函数,v,n为过程噪声和测量噪声,噪声都是独立同分布的。上面对应的那个例子将会出现在程序中。
从贝叶斯理论的观点来看,状态估计问题(目标跟踪、信号滤波)就是根据之前一系列的已有数据(后验知识)递推的计算出当前状态
的可信度。这个可信度就是概率公式
,它需要通过预测和更新两个步奏来递推的计算。
预测过程是利用系统模型(状态方程1)预测状态的先验概率密度,也就是通过已有的先验知识对未来的状态进行猜测,即p( x(k)|x(k-1) )。更新过程则利用最新的测量值对先验概率密度进行修正,得到后验概率密度,也就是对之前的猜测进行修正。
在处理这些问题时,一般都先假设系统的状态转移服从一阶马尔科夫模型,即当前时刻的状态x(k)只与上一个时刻的状态x(k-1)有关。这是很自然的一种假设,就像小时候玩飞行棋,下一时刻的飞机跳到的位置只由当前时刻的位置和骰子决定。同时,假设k时刻测量到的数据y(k)只与当前的状态x(k)有关,如上面的状态方程2。
为了进行递推,不妨假设已知k-1时刻的概率密度函数
预测:由上一时刻的概率密度得到
,这个公式的含义是既然有了前面1:k-1时刻的测量数据,那就可以预测一下状态x(k)出现的概率。
计算推导如下:
等式的第一行到第二行纯粹是贝叶斯公式的应用。第二行得到第三行是由于一阶马尔科夫过程的假设,状态x(k)只由x(k-1)决定。
楼主看到这里的时候想到两个问题:
第一:既然 ,x(k)都只由x(k-1)决定了,即
,在这里弄一个
是什么意思?
这两个概率公式含义是不一样的,前一个是纯粹根据模型进行预测,x(k)实实在在的由x(k-1)决定,后一个是既然测到的数据和状态是有关系的,现在已经有了很多测量数据 y 了,那么我可以根据已有的经验对你进行预测,只是猜测x(k),而不能决定x(k)。
第二:上面公式的最后一行是假设已知的,但是
怎么得到呢?
其实它由系统状态方程决定,它的概率分布形状和系统的过程噪声
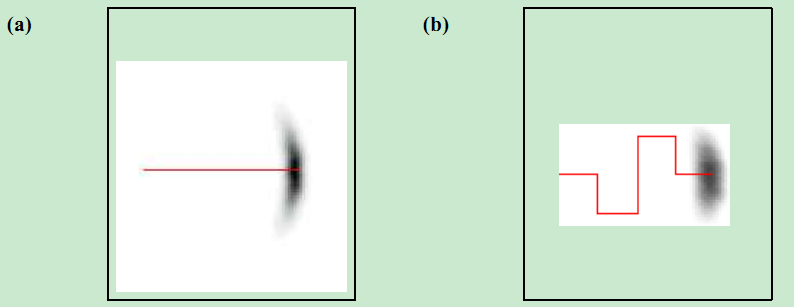
形状一模一样。如何理解呢?观察状态方程(1)式我们知道,x(k) = Constant( x(k-1) ) + v(k-1) 也就是x(k)由一个通过x(k-1)计算出的常数叠加一个噪声得到。看下面的图:
如果没有噪声,x(k)完全由x(k-1)计算得到,也就没由概率分布这个概念了,由于出现了噪声,所以x(k)不好确定,他的分布就如同图中的阴影部分,实际上形状和噪声是一样的,只是进行了一些平移。理解了这一点,对粒子滤波程序中,状态x(k)的采样的计算很有帮助,要采样x(k),直接采样一个过程噪声,再叠加上 f(x(k-1)) 这个常数就行了。
更新:由得到后验概率
。这个后验概率才是真正有用的东西,上一步还只是预测,这里又多了k时刻的测量,对上面的预测再进行修正,就是滤波了。这里的后验概率也将是代入到下次的预测,形成递推。
推导:
其中归一化常数:
等式第一行到第二行是因为测量方程知道, y(k)只与x(k)有关,也称之为似然函数,由量测方程决定。也和上面的推理一样,
, x(k)部分是常数,
也是只和量测噪声n(k)的概率分布有关,注意这个也将为SIR粒子滤波里权重的采样提供编程依据。
贝叶斯滤波到这里就告一段落了。但是,请注意上面的推导过程中需要用到积分,这对于一般的非线性,非高斯系统,很难得到后验概率的解析解。为了解决这个问题,就得引进蒙特卡洛采样。关于它的具体推导请见 下一篇博文。
(转载请注明作者和出处:http://blog.csdn.net/heyijia0327 未经允许请勿用于商业用途)
reference:
1.M. Sanjeev Arulampalam 《A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking》
2.ZHE CHEN 《Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond》
3.Sebastian THRUN 《Probabilistic Robotics》
3.百度文库 《粒子滤波理论》





















 4172
4172











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








